Yandex.Algorithm 2017 Qualification Round Editorial
Problemset was prepared by Yandex employees from Minsk.
Problem А. Task Management
Consider a solution with the complexity 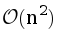 . Use a variable to track the last closed task and go through the list of tasks from the beginning to the end. Increase the counter when passing through the element corresponding to the next task. The constrains are quite large, so this solution doesn’t fit the timelimit.
. Use a variable to track the last closed task and go through the list of tasks from the beginning to the end. Increase the counter when passing through the element corresponding to the next task. The constrains are quite large, so this solution doesn’t fit the timelimit.
What is the case when we can not find any suitable tasks up to the end of the list? There is only one case: the task number (x+1) is closer to the beggining of the list then the closed task number x. Therefore, to solve the problem we can determine position of each task in the task list and count the number of distinct numbers x such that the position of task number (x+1) is less than the position of task number x.
Don’t forget to consider the first pass through the task list. The final complexity of the solution is 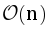 .
.
Problem B. Cross-City Communication
Problem ’’Cross-City Communication`` does not contain any special algorithmic ideas, so we have to implement behavior described in the problem statement.
For each hour from 0 to 23 we need to check the free conference rooms in the reqired cities.
Note that for larger constrains determining of free conference room for each pair (city, hour) can help to answer queries faster. This information allows to answer a query in time proportional to the number of cities instead of the total number of conference rooms.
Problem C. Test Invocation
There are several different approaches to solve the problem, consider two of them.
The first solution is based on counting the number of times the test number x will be run. In the original system each test runs once, and in the new system it runs 2d(x) times, where d(x) is the distance from the root test to test number x. This can be easily proved by the induction (this fact can be guessed from the description of the samples). d(x) can be calculated by any traversal of the tree.
The second approach is based on dynamic programming. Let T(x) be equal to the total running time of the test number x, i.e. sum of the running timeS of the tests it depends and the checking time ax. So we have:
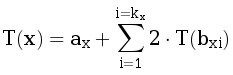
To compute the answer T(1) we run a tree traversal and calculate T(x) values using the recurrent formula above.
The complexity of solution is 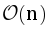 .
.
Problem D. Artihmetic Mean Encoding
Сonsider next problem. If n = b1 + b2 + … + bc and all bi are powers of two with non-negative integer exponents, find all possible values of c. We will show that c can be equal to any integer from popcount(n) to n (where popcount(n) is the number of set bits in binary representation of n).
It is obvious that we cannot use less than popcount(n) numbers and more than n. If we have a sequence bi of length x (x < n) it always contains an element 2t with a positive value t. We can replace it with the two elements 2t-1, obtaining a sequence of length (x+1). The sequence bi of length popcount(n) can be build from the binary representation of the number n.
To solve the problem we can start from k equals to 1 and check existence of the sequence ai. As shown above, we need to find the minimum k that popcount(kn) ≤ k and construct the answer.
For problem constraints k does not exceed 60 (60 ⋅ (250 - 1) < 260 - 1 = 20 + 21 + … + 259).
Problem E. Cluster Connection
Graph should not contain brigdes, so the degree of each vertice is not less than two. Since the sum of degree of all vertices is equal to 2 ⋅ n + 2 we have two possible cases:
- there is one vertex of degree 4;
- there are two vertices of degree 3.
Consider the first case. Graph is an union of two cycles of length (m + 1) and (n - m) with a common vertex. In this case, we need to choose which vertices will be in the first cycle (other will go to the second), and the order in which vertices will be on these cycles. The number of ways to construct such graph is
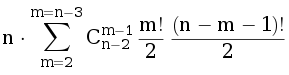
Consider the second case. In the graph there are two vertices of degree three connected by chains of edges. All the other (n-2) vertices are located on this chains. Note that there can be only one connection with zero additional vertices (an edge). Let the chains have a, b and c vertices are (a ≤ b ≤ c). Consider a few cases:
- 0 ≤ a < b < c, then the number of graphs is equal to
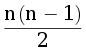
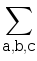 C(n-2, a) C(n - 2 - a, b)
C(n-2, a) C(n - 2 - a, b) 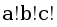 ;
; - 0 < a = b < c, then the number of graphs is equal to
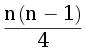
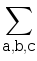 C(n-2, a) C(n - 2 - a, b)
C(n-2, a) C(n - 2 - a, b) 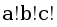 ;
; - 0 ≤ a < b = c, then the number of graphs is equal to
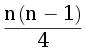
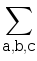 C(n-2, a) C(n - 2 - a, b)
C(n-2, a) C(n - 2 - a, b) 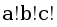 ;
; - 0 < a = b = c, then the number of graphs is equal to
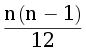
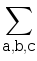 Cn-2a C(n - 2 - a, b)
Cn-2a C(n - 2 - a, b) 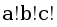 .
.
Combine all formulas together and obtain the final result.
Problem F. Repetitions
To solve this problem, refer to the string terminology. A border of a string s is some string y that x starts with and ends with y.
For each prefix p of the text we need to find the maximum length of the border, which has at least one additional occurrence in this prefix. To do this, we can find all borders of p, go through this list in descending order of lengths to find the first with additional occurence.
To search for all borders we can use the prefix-function. Additionally, remembering that 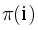 is the maximal border of the prefix with length i, and length of all the borders form sequence
is the maximal border of the prefix with length i, and length of all the borders form sequence 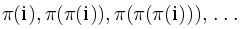 etc.
etc.
Interesting fact: the border of length 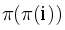 always has at least three occurrences in the prefix with length i (the first starts in the first position, the second ends in the position i and the third ends in position
always has at least three occurrences in the prefix with length i (the first starts in the first position, the second ends in the position i and the third ends in position 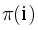 ).
).
To find the answer of the problem we need the way to check whether the additional entry of the maximum length border (of length 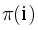 ) exists. If such occurrence exists then text has a position j (j < i), where
) exists. If such occurrence exists then text has a position j (j < i), where 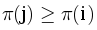 . For a quick check of this inequality, it is sufficient to compute the prefix maximum values of the prefix-function.
. For a quick check of this inequality, it is sufficient to compute the prefix maximum values of the prefix-function.
The complexity of algorithm is 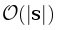 .
.